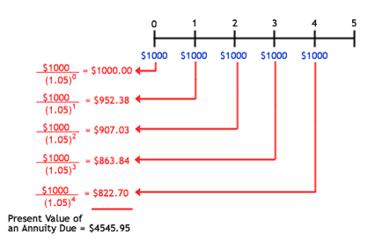
Аннуитетной называют схему выплаты задолженности, когда размер взноса за определенный период (обычно 1 месяц) остается неизменным.

Любой платеж по аннуитетной схеме включает в себя выплату процентов за пользование средствами и возврат тела кредита. Отличительной чертой такого графика погашения задолженности является то, что в самом начале выплат большую часть платежа составляют именно проценты, поэтому сумма основного долга уменьшается медленно. Итоговая переплата при выборе аннуитетных платежей оказывается намного выше, чем по дифференцированной схеме. Однако, есть у аннуитетной схемы и свои преимущества — она оказывает намного меньшую нагрузку на бюджет заемщика, поэтому снижается вероятность невозврата долга.

Сегодня именно аннуитетная схема является наиболее популярной, большинство банков используют ее по умолчанию. Объясняется это выгодой для финансового учреждения: меньшим риском невыполнения долговых обязательств и повышенным заработком. Другим достоинством аннуитетных платежей можно назвать более простое обслуживание, ведь нет необходимости ежемесячно рассчитывать сумму платежа, кроме того, заемщику проще планировать личный бюджет, основываясь на постоянном размере выплат по кредиту.

Размер ежемесячного платежа по аннуитетной схеме рассчитывается по следующей формуле = ОСЗ х ПС / [1 - (1 + ПС)^-ПП], где:

ОСЗ – остаток ссудной задолженности, то есть сумма долга, которую еще осталось погасить на момент внесения платежа.

ПС – месячная процентная ставка за пользование деньгами, она составляет 1/12 от годовой ставки. В расчете используется ставка, установленная в кредитном договоре для займов с постоянной ставкой, и актуальная процентная ставка на момент внесения платежа для займов с переменной или смешанной ставкой.

ПП – число процентных периодов (чаще всего используются месяцы), которые остались до момента полной выплаты кредита в соответствии с установленным графиком.

В качестве примера расчетов суммы аннуитетного платежа будет использован кредитный договор со следующими параметрами:

1. общая сумма кредита – 5000 руб.(данный параметр соответствует ОСЗ на момент первой выплаты);
2. процентная ставка по кредиту - 15 % в год, таким образом ежемесячная ставка равняется 15%/12 = 1.25% (ПС);
3. срок полной выплаты кредита – 6 месяцев (ПП = 6, в качестве процентного периода выступает месяц).

На основании этих данных можно рассчитать размер ежемесячного платежа:

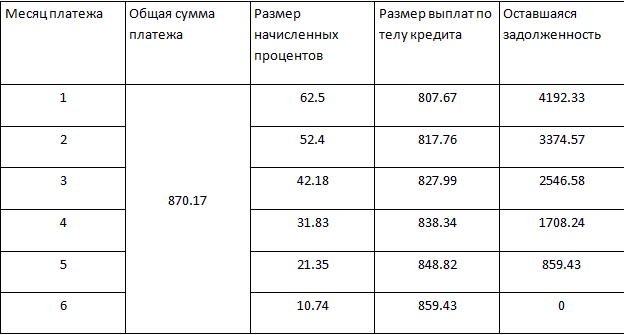
Сумма месячных процентов = ОСЗ * ПС / 100 %, в первый месяц она равна 5000 * 1.25/100% = 62.5 руб.

Общий размер платежа составит 62.5/[1-(1.0125)^-6] = 870.17 руб.

В табличных данных прослеживается четкая зависимость — чем длительнее выполняются выплаты займа, тем меньше сумма процентов и больше часть, идущая на погашение тела кредита.

Общая сумма выплат по кредиту составит 5221 руб. Из них 221 руб. ушли на выплату процентов за пользование средствами. В случае дифференцированного платежа общая сумма процентов составила бы 218.75 руб. На сумме в 5000 руб. переплата кажется небольшой, однако, при покупке квартиры или автомобиля разница будет весьма существенной.

Разумеется, заемщику не требуется самостоятельно рассчитывать график выплат, в большинстве случаев на сайте банка присутствует специальный кредитный калькулятор, который делает это в автоматическом режиме. Зачем же тогда нужна эта формула? Прежде всего, чтобы проверить банк, а также самостоятельно ознакомиться с преимуществами и недостатками существующих графиков платежей, чтобы принять взвешенное решение без помощи финансовых специалистов.

Похожие материалы:

• Закладная
• Дифференцируемый платеж

• -1
• Tweet